We consider the First Law of Thermodynamics applied to stationary closed systems as a conservation of energy principle. Thus energy is transferred between the system and the surroundings in the form of heat and work, resulting in a change of internal energy of the system. Internal energy change can be considered as a measure of molecular activity associated with change of phase or temperature of the system and the energy equation is represented as follows:
Heat (Q)
Energy transferred across the boundary of a system in the form of heat always results from a difference in temperature between the system and its immediate surroundings. We will not consider the mode of heat transfer, whether by conduction, convection or radiation, thus the quantity of heat transferred during any process will either be specified or evaluated as the unknown of the energy equation. By convention, positive heat is that transferred from the surroundings to the system, resulting in an increase in internal energy of the system
Work (W)
In this course we consider three modes of work transfer across the boundary of a system, as shown in the following diagram:
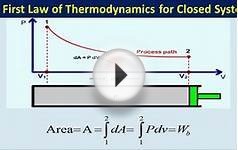
In this course we are primarily concerned with Boundary Work due to compression or expansion of a system in a piston-cylinder device as shown above. In all cases we assume a perfect seal (no mass flow in or out of the system), no loss due to friction, and quasi-equilibrium processes in that for each incremental movement of the piston equilibrium conditions are maintained. By convention positive work is that done by the system on the surroundings, and negative work is that done by the surroundings on the system, Thus since negative work results in an increase in internal energy of the system, this explains the negative sign in the above energy equation.